The weekdays of the March 14 - March 20 week were quite calm, but that was more than compensated by the super packed weekend.
Before we dive further into that March week, though, let me remind you that Google Code Jam Qualification Round starts in a few minutes. Google Code Jam's problems are always among the most interesting (yeah, I'm biased since I help create them, too), so consider giving it a try! You can already register, and the problems will appear in a few minutes. This round lasts for 27 hours, but you don't need to be present all that time - a few hours at a convenient time should work just fine. Good luck!
The competitive programming extravaganza started Friday evening with the Elimination Round of the 2016 CROC Championship on Codeforces (problems, results, top 5 on the left, parallel round results). The deciding problem G, quite surprisingly, involved high-school-style geometry.
You were given a set of 100000 points, and needed to draw a line through some two of them. The line you draw must have the lowest imbalance out of all possibilities. The imbalance of a line is defined as the maximum over all points X on that line of |XP-XQ|, where P and Q are two additional given fixed points.
At the first sight, this looks like a very strange definition. However, as you progress through the layers of this problem, the solution ends up being quite exciting, so I encourage you to try :)
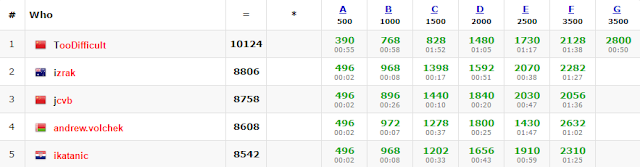
Early on Saturday, Codeforces ran another company round, called IndiaHacks 2016 (problems, results, top 5 on the left). Once again TooDifficult earned the most points; note that he did earn the most in the above CROC round too, he was just participating in the parallel unofficial track — congratulations!
A bit later on Saturday an onsite Swiss competition called Helvetic Coding Contest 2016 took place in Lausanne (results, top 5 on the left). To the best of my knowledge, the problems will be used for an online contest soon, so I will not spoil them.
Instead, I'd like to mention that it's really nice to see such "local" competitions spread all over the world, helping build algorithmic programming communities and thus enabling the enthusiasts to make new friends and discover new opportunities. Thanks a lot for the organizers from EPFL PolyProg for this exciting event!
TopCoder SRM 685 wrapped up the Saturday (problems, results, top 5 on the left). ACRush has continued his climb back to the top of the rankings, but it was matthew99a who did the best this time — congratulations to all winners!
And finally, Open Cup 2015-16 Grand Prix of Baltics wrapped up the week on Sunday (results, top 5 on the left). Without Warsaw Eagles participating, team Past Glory is unstoppable — congratulations on another victory!
Problem B was the most exciting in this round for me. You were given a 8x8 grid, with three points on this grid designated as "houses", and three as "wells". You need to pick a positive integer d<=1000, subdivide each square of the grid into d times d small squares, obtaining a 8d times 8d grid, and then draw nine non-intersecting paths on this grid: from each house to each well. Of course, the problem as stated is impossible to solve since K3,3 is not planar; to make it solvable, the grid was toroidal: the left edge was identified with the right edge, and the top edge was identified with the bottom edge.
Every time a problem requires one to come up with some not necessarily optimal structure (for example in this problem the paths don't have to be the shortest), the added freedom usually means that the solution requires more creativity than usual, so I hope you will enjoy solving it! To test your solution, you can just generate random locations of houses and wells on the 8x8 grid many times.
I've mentioned two interesting problems in my last summary. The first one was quite unusual:you're given an array of N<=50 positive integers, summing up to M<=1000. For each of N! possible permutations of the array, we compute the value M!/(a[0]+a[1])/(a[0]+a[1]+a[2])/.../(a[0]+a[1]+...+a[N-1]) - dividing M! by the product of partial sums of the permuted array, except the first one. What is the sum of those values over all N! permutations?
First, we try to solve the problem where the first partial sum is not skipped, in other words when the expression above is also divided by a[0]. Instead of dividing the factorial by the partial sums, we'll simply remove the corresponding numbers a[0], a[0]+a[1], ..., a[0]+a[1]+...+a[N-1] from the factorial's product. The last removed number is M=a[0]+a[1]+...+a[N-1], the next one is M-a[N-1], and so on. Which combinatorial objects does such a product count?
Experienced contestants might recognize the pattern of almost-factorial with some numbers skipped. It arises when we try to count permutations by cycles. Suppose we have a permutation on numbers between 1 and M. Consider its cycle passing through 1. There are M-1 choices for the next element in the cycle, M-2 choices for the element after it, which corresponds to our product, and when the number M-a[N-1] is skipped, we say that the cycle goes back to number 1, and then we consider the cycle passing through the smallest untouched number, and so on until we build all cycles.
So our product counts permutations where the cycle passing through 1 has a[N-1] elements, the cycle passing through the smallest number untouched by the first cycle has a[N-2] elements, and so on. When we sum those products over all permutations of array a, we simply get the total number of permutations with the given cycle lengths (a[0], a[1], ..., a[N-1]), where cycles of the same length also have an order on them.
This is where the key simplification happened: after summing by all permutations of a, we actually have to count combinatorial objects that are easier to describe! To solve the problem, we must now adjust for the divisor a[0] being missing (hint: now instead of counting permutations, we need to sum the lengths of the cycle with the largest smallest number), and learn how to count the sum quickly (hint: dynamic programming with state "how many cycles we've already processed, what is the position of the number that is destined to become the largest smallest number in a cycle").
The second problem from the last summary was more standard, but not less beautiful: you're given two strings of 0s and 1s with at most 10000 characters in each. You're allowed to take any substring of a string which has an even amount of 1s, and reverse it. Can you obtain the second string from the first string?
Let's go from left to right, and find the first positions where the strings don't match: one of them has a 0 in that position, and the other has a 1. Let's find the next two ones in the string that contains 0 there, and reverse the substring starting with this 0 and ending with the second one. Now both strings have ones in this position, and we can continue going to the right.
When would this approach stop working? When there's less than two ones left in one of the strings (and thus in the other, too, if they have the same amount of ones). It's tempting to say that if the sole remaining ones in the two strings match, then we're done, otherwise there's no solution. But how to prove that?
During the actual competition, our team tried to prove this for some time, failed to do so, tried to come up with a counterexample, also failed to do so, and decided to take chances and submit this solution - and it was accepted!
After the competition ended, we were still very much interested to prove why this solution works, and finally found the invariant: if we look at positions of ones in the string, and make an alternating sum out of them (p1-p2+p3-p4+...), then the value of this alternating sum doesn't change when we flip a string with an even amount of ones in it! And it's quite obvious that this sum is different when all ones match except one.
Thanks for reading, and check back soon for more algorithms!
Before we dive further into that March week, though, let me remind you that Google Code Jam Qualification Round starts in a few minutes. Google Code Jam's problems are always among the most interesting (yeah, I'm biased since I help create them, too), so consider giving it a try! You can already register, and the problems will appear in a few minutes. This round lasts for 27 hours, but you don't need to be present all that time - a few hours at a convenient time should work just fine. Good luck!
The competitive programming extravaganza started Friday evening with the Elimination Round of the 2016 CROC Championship on Codeforces (problems, results, top 5 on the left, parallel round results). The deciding problem G, quite surprisingly, involved high-school-style geometry.
You were given a set of 100000 points, and needed to draw a line through some two of them. The line you draw must have the lowest imbalance out of all possibilities. The imbalance of a line is defined as the maximum over all points X on that line of |XP-XQ|, where P and Q are two additional given fixed points.
At the first sight, this looks like a very strange definition. However, as you progress through the layers of this problem, the solution ends up being quite exciting, so I encourage you to try :)
Early on Saturday, Codeforces ran another company round, called IndiaHacks 2016 (problems, results, top 5 on the left). Once again TooDifficult earned the most points; note that he did earn the most in the above CROC round too, he was just participating in the parallel unofficial track — congratulations!
A bit later on Saturday an onsite Swiss competition called Helvetic Coding Contest 2016 took place in Lausanne (results, top 5 on the left). To the best of my knowledge, the problems will be used for an online contest soon, so I will not spoil them.
Instead, I'd like to mention that it's really nice to see such "local" competitions spread all over the world, helping build algorithmic programming communities and thus enabling the enthusiasts to make new friends and discover new opportunities. Thanks a lot for the organizers from EPFL PolyProg for this exciting event!
TopCoder SRM 685 wrapped up the Saturday (problems, results, top 5 on the left). ACRush has continued his climb back to the top of the rankings, but it was matthew99a who did the best this time — congratulations to all winners!
And finally, Open Cup 2015-16 Grand Prix of Baltics wrapped up the week on Sunday (results, top 5 on the left). Without Warsaw Eagles participating, team Past Glory is unstoppable — congratulations on another victory!
Problem B was the most exciting in this round for me. You were given a 8x8 grid, with three points on this grid designated as "houses", and three as "wells". You need to pick a positive integer d<=1000, subdivide each square of the grid into d times d small squares, obtaining a 8d times 8d grid, and then draw nine non-intersecting paths on this grid: from each house to each well. Of course, the problem as stated is impossible to solve since K3,3 is not planar; to make it solvable, the grid was toroidal: the left edge was identified with the right edge, and the top edge was identified with the bottom edge.
Every time a problem requires one to come up with some not necessarily optimal structure (for example in this problem the paths don't have to be the shortest), the added freedom usually means that the solution requires more creativity than usual, so I hope you will enjoy solving it! To test your solution, you can just generate random locations of houses and wells on the 8x8 grid many times.
I've mentioned two interesting problems in my last summary. The first one was quite unusual:you're given an array of N<=50 positive integers, summing up to M<=1000. For each of N! possible permutations of the array, we compute the value M!/(a[0]+a[1])/(a[0]+a[1]+a[2])/.../(a[0]+a[1]+...+a[N-1]) - dividing M! by the product of partial sums of the permuted array, except the first one. What is the sum of those values over all N! permutations?
First, we try to solve the problem where the first partial sum is not skipped, in other words when the expression above is also divided by a[0]. Instead of dividing the factorial by the partial sums, we'll simply remove the corresponding numbers a[0], a[0]+a[1], ..., a[0]+a[1]+...+a[N-1] from the factorial's product. The last removed number is M=a[0]+a[1]+...+a[N-1], the next one is M-a[N-1], and so on. Which combinatorial objects does such a product count?
Experienced contestants might recognize the pattern of almost-factorial with some numbers skipped. It arises when we try to count permutations by cycles. Suppose we have a permutation on numbers between 1 and M. Consider its cycle passing through 1. There are M-1 choices for the next element in the cycle, M-2 choices for the element after it, which corresponds to our product, and when the number M-a[N-1] is skipped, we say that the cycle goes back to number 1, and then we consider the cycle passing through the smallest untouched number, and so on until we build all cycles.
So our product counts permutations where the cycle passing through 1 has a[N-1] elements, the cycle passing through the smallest number untouched by the first cycle has a[N-2] elements, and so on. When we sum those products over all permutations of array a, we simply get the total number of permutations with the given cycle lengths (a[0], a[1], ..., a[N-1]), where cycles of the same length also have an order on them.
This is where the key simplification happened: after summing by all permutations of a, we actually have to count combinatorial objects that are easier to describe! To solve the problem, we must now adjust for the divisor a[0] being missing (hint: now instead of counting permutations, we need to sum the lengths of the cycle with the largest smallest number), and learn how to count the sum quickly (hint: dynamic programming with state "how many cycles we've already processed, what is the position of the number that is destined to become the largest smallest number in a cycle").
The second problem from the last summary was more standard, but not less beautiful: you're given two strings of 0s and 1s with at most 10000 characters in each. You're allowed to take any substring of a string which has an even amount of 1s, and reverse it. Can you obtain the second string from the first string?
Let's go from left to right, and find the first positions where the strings don't match: one of them has a 0 in that position, and the other has a 1. Let's find the next two ones in the string that contains 0 there, and reverse the substring starting with this 0 and ending with the second one. Now both strings have ones in this position, and we can continue going to the right.
When would this approach stop working? When there's less than two ones left in one of the strings (and thus in the other, too, if they have the same amount of ones). It's tempting to say that if the sole remaining ones in the two strings match, then we're done, otherwise there's no solution. But how to prove that?
During the actual competition, our team tried to prove this for some time, failed to do so, tried to come up with a counterexample, also failed to do so, and decided to take chances and submit this solution - and it was accepted!
After the competition ended, we were still very much interested to prove why this solution works, and finally found the invariant: if we look at positions of ones in the string, and make an alternating sum out of them (p1-p2+p3-p4+...), then the value of this alternating sum doesn't change when we flip a string with an even amount of ones in it! And it's quite obvious that this sum is different when all ones match except one.
Thanks for reading, and check back soon for more algorithms!






No comments:
Post a Comment